PROJECTILE
• Projectile is the name given to
a body thrown with some initial velocity, and then allowed to move in two
dimensions under the action of gravity alone, without being propelled by any
engine or fuel. The path followed by a projectile is called its trajectory.
Examples of projectiles
• A
cricket ball hit by a bat.
• A
javelin or hammer thrown by an athlete.
• A
bullet fired from a rifle.
• A
piece of stone thrown in any direction.
ASSUMPTIONS IN PROJECTILE MOTION
There is no frictional resistance of air.
• The
effect due to rotation of earth and curvature of the earth is negligible.
• The
acceleration due to gravity is constant in magnitude and direction at all
points of the motion of projectile.
ANGULAR PROJECTION
• OX,is
a horizontal line on ground and
• OY is a vertical line perpendicular to ground.
• Suppose a cricket ball be projected from the
point O with velocity u, making an angle θ with the horizontal
direction OX
Resolving
velocity into two rectangular
components, we get
(i) u cosθ , along OX
(ii) u sin θ along OY.
• As these two component velocities act at right
angles to each other, therefore they are independent of each other.
The horizontal component velocity u cos θ
is constant throughout the motion as there is no accelerating force in
the horizontal direction.
The vertical component velocity u
sinθ decreases continuously with height, from O
to H, due to downward force of gravity and becomes zero at H.
EQUATION OF TRAJECTORY:
Path of projectile
• Suppose
at any time t, the object reaches at P (x, y) clearly,
• x=
horizontal distance traveled by object in time t
• y
= vertical distance traveled by object in time t.
This is an equation of a parabola
Time of flight
• .
It is the total time for which the object is in flight (i.e. remains in
air). It is denoted by T.
• The
total time of flight consists of two parts
• Total time of flight = time of ascent
+ time of descent
Maximum height
It is the maximum vertical height attained by the object
above the point of projection during its flight. It is denoted by h.
| Horizontal Range : | It is the horizontal distance covered by the object between its point of projection and the point of hitting the ground. It is denoted by R. |
Clearly,
the horizontal range is the horizontal distance covered by the object with
uniform velocity u cosθ in the time equal to total time of flight T.
Maximum Horizontal Range
• we note that for a given speed u of the object, the value of horizontal range depends upon angle of projection as g is constant at a place. Therefore horizontal range R will be maximum if
• Sin 2θ = maximum = 1
• = sin 90°
• Or 2θ =90° or θ =45°
• This concept has been used by athletes in long jump, javelin throw, cricket ball throw etc


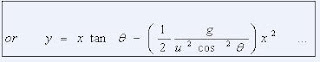




No comments:
Post a Comment