28.1. Electric Current
Figure 28.1. Electric field in a wire.
When a wire is connected to the terminals of a battery, an
electric field is generated inside the wire (see Figure 28.1). The free
electrons in the wire will move in a direction opposite to that of the field
lines. The electric charge will try to redistribute itself in such a way that
the net electric field in the wire is equal to zero. However, the positive
terminal of a battery acts as a sink for electrons and the negative terminal
acts as a source of electrons, and a continuous flow of electrons will be
created. This continuous flow of electrons is called an
electric
current. The symbol of current is I and its SI unit is the Ampere (A).
The current is defined as
(28.1)
where dq is the amount of charge that flows past some given point on the wire
during a time period dt. A current of 1 A is equal to 1 C/s. The
current density j is defined as
(28.2)
where I is the current flowing through the conductor, and A is the
cross-sectional area of the conductor. Even though the electrons feel an
electric field inside the conductor, they will not accelerate. The electrons
will experience significant friction as a result of collisions with the
positive ions in the conductor. On average, the electrons will move with a
constant speed from the negative terminal of the battery to the positive
terminal. Their average velocity, also called the drift velocity
v
d, is proportional to the electric field E
(28.3)
For a given density of electrons in the conductor, an increase of the drift
velocity of each of the electrons will increase the number of electrons passing
by a given point on the conductor per unit of time. This is illustrated in
Figure 28.2. During a time interval dt the electrons will cover, on average, a
distance equal to dx where
(28.4)
Figure 28.2. Motion of average electron in conductor.
All electrons within a distance dx from the point P will
therefore pass this point during the time interval dt. Suppose the density of
electrons in the conductor is n electrons/m
3. The number of
electrons dN that will pass P during the time interval dt is then equal to
(28.5)
Since each electron carries a charge e, the total charge dQ that will pass
point P in a time interval dt is equal to
(28.6)
The current through the conductor is therefore equal to
(28.7)
Equation (28.7) shows that the current in the conductor is proportional to the
cross-sectional area of the conductor and proportional to the drift velocity.
Since the drift velocity is proportional to the electric field E the following
relation holds for the current in the conductor:
(28.8)
The electric field in the conductor is determined by its length L and the
potential difference [Delta]V between its two ends (E = [Delta]V/L).
Equation (28.8) can therefore be rewritten as
(28.9)
Equation (28.9) can be rewritten as
(28.10)
The constant of proportionality [rho] is called the resistivity of the
material. The resistivity [rho] depends on the characteristics of the
conductor ([rho] is small for a good conductor, and [rho] is very large for an
insulator). The resistance R of a conductor is defined as
(28.11)
The SI unit of resistance is the ohm ([Omega]). Using the resistance R we can
rewrite eq.(28.10)
(28.12)
Equation (28.12) is called
Ohm's Law. Equation (28.12) shows
that the current through a conductor is proportional to the potential
difference between the ends of the conductor and inversely proportional to its
resistance. Equation (28.12) also shows that 1 [Omega] equals 1 V/A.
Example: Problem 28.5
An aluminum wire has a resistance of 0.10 [Omega]. If you draw this
wire through a die, making it thinner and twice as long, what will be its new
resistance ?
The initial resistance R
i of the aluminum wire with length L and
cross-sectional area A is equal to
(28.13)
The initial volume of the wire is L
. A. After passing the wire
through the die, it s length has changed to L' and its cross-sectional area is
equal A'. Its final volume is therefore equal to L' A'. Since the density of
the aluminum does not change, the volume of the wire does not change, and
therefore the initial and final dimensions of the wire are related:
(28.14)
or
(28.15)
The problem states that the length of the wire is doubled (L' = 2 L). The
final cross-sectional area A' is therefore related to the initial
cross-sectional area A in the following manner:
(28.16)
The final resistance R
f of the wire is given by
(28.17)
The resistance of the wire has increased by a factor of four and is now 0.40
[Omega].
28.2. The resistivity of materials
The resistivity [rho] has as units ohm-meter ([Omega]
. m). The
resistivity of most
conductors is between 10
-8 [Omega]
. m and 10
-7 [Omega]
. m. The resistivity of
a conductor depends not only on the type of the material but also on its
temperature. The resistivity of an
insulator varies between
10
11 [Omega]
. m and 10
17 [Omega]
.
m. In all materials the resistivity decreases with decreasing temperature. In
some materials, such as lead, zinc, tin and niobium, the resistivity vanishes
as the temperature approaches absolute zero. At these low temperatures, these
materials exhibit
superconductivity.
Example: Problem 28.17
The air conditioner in a home draws a current of 12 A. Suppose that
the pair of wires connecting the air conditioner to the fuse box are No. 10
copper wires with a diameter of 0.259 cm and a length of 25 m each.
a) What is the potential drop along each wire ? Suppose that the voltage
delivered to the home is exactly 110 V at the fuse box. What is the voltage
delivered to the air conditioner ?
b) Some older homes are wired with No. 12 copper wire with a diameter of 0.205
cm. Repeat the calculation of part (a) for this wire.
Figure 28.3. Wiring diagram of air conditioner in problem
28.17.
a) The resistivity of copper is 1.7 x 10
-8 [Omega]
. m
(see Table 28.1). The resistance R
Cu of each copper wire is equal
to
(28.18)
where L is the length of the wire and d is its diameter. A current I is
flowing through the wires and I = 12 A. The voltage drop [Delta]V across each
wire is equal to
(28.19)
Figure 28.3 shows schematically a wiring diagram of the air conditioner
circuit. The voltage across the air-conditioner unit is equal to 110 - 2
. [Delta]V, where [Delta]V is given by eq.(28.19). The length of
each copper cable is 25 m, and its diameter is equal to 0.259 cm. The voltage
drop across each wire is thus equal to
(28.20)
The voltage across the AC unit is therefore equal to 108.1 V.
b) A No. 12 wire has a diameter equal to 0.205 cm. The voltage drop across
this wire is equal to
(28.21)
and the voltage across the AC unit is equal to 106.9 V.
Example: Problem 28.12
A high voltage transmission line has an aluminum cable of diameter 3.0
cm, 200 km long. What is the resistance of this cable ?
The resistivity of aluminum is 2.8 x 10
-8 [Omega] m. the length of
the cable is 200 km or 2 x 10
5 m. The diameter of the cable is 3 cm
and its cross-sectional area is equal to [pi] (d/2)
2 or 7.1 x
10
-4 m
2. Substituting these values into eq.(28.11) the
resistance of the cable can be determined
(28.22)
28.3. Resistance in combination
A device that is specifically designed to have a high resistance is called a
resistor. The symbol of a resistor in a circuit diagram is a zigzag line (see
Figure 28.4).
Figure 28.4. Symbol of a resistor.
Figure 28.5 shows two resistors with resistance R
1
and R
2 connected in series. Suppose the current flowing through the
circuit is equal to I. The voltage drop [Delta]V
1 across resistor
R
1 is equal to
(28.23)
and the voltage drop [Delta]V
2 across resistor R
2 is
equal to
(28.24)
The potential difference [Delta]V across the series circuit is equal to
(28.25)
Equation (28.25) shows that two resistors connected in series act like one
resistor with a resistance equal to the sum of the resistance of resistor 1 and
the resistance of resistor 2
(28.26)
Figure 28.5. Two resistors connected in series.
Figure 28.6 shows two resistors connected in parallel. In
this circuit, the current through each resistor will be different, but the
voltage drop [Delta]V across each resistor will be the same. Using Ohm's law
the current I
1 flowing through resistor R
1 can be
calculated
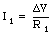
(28.27)
and the current I
2 flowing through resistor R
2 is equal
to
(28.28)
The total current flowing through the circuit is equal to the sum of the
currents through each resistor
(28.29)
The resistor network shown in Figure 28.6 is therefore equivalent to a single
resistor R where R can be obtained from the following relation
(28.30)
Equation (28.30) shows that the resistance of a parallel combination of
resistors is always less than the resistance of each of the individual
resistors.
Figure 28.6. Two resistor connected in parallel.
Example: Problem 28.41
Commercially manufactured superconducting cables consist of filaments
of superconducting wire embedded in a matrix of copper. As long as the
filaments are superconducting, all the current flows in them, and no current
flows in the copper. But if the superconductivity suddenly fails because of a
temperature increase, the current can spill into the copper; this prevents
damage to the filaments of the superconductor. Calculate the resistance per
meter of length of a copper matrix. The copper matrix has a diameter of 0.7
mm, and each of the 2100 filaments has a diameter of 0.01 mm.
Consider 1 meter of cable. The cross-sectional area of each filament is [pi]
. (d/2)
2 = 7.9 x 10
-11 m
2. The
cross-sectional area of 2100 filaments is equal to 1.65 x 10
-7
m
2. The diameter of the copper matrix is equal to 0.7 mm, and its
cross-sectional area is equal to 1.54 x 10
-6 m
2. The
area of the copper itself is thus equal to 1.37 x 10
-6
m
2. The resistance of the copper matrix per unit length is equal
to
(28.31)
Suppose the resistivity of the filament at room temperature is the same as the
resistivity of copper. The resistance of each superconducting filament is
equal to
(28.32)
The wire can be treated as a parallel circuit of one resistor representing the
resistance of the copper matrix and 2100 resistors representing the 2100
strands of superconducting wire. The fraction of the current flowing through
the copper matrix can be determined easily. Suppose that the potential
difference across the conductor is equal to [Delta]V. The current
I
Cu flowing through the copper matrix is equal to
(28.33)
The current I
fil flowing through the 2100 filaments is equal to
(28.34)
The fraction F of the total current flowing through the copper matrix is equal
to
(28.35)
Two special cases will need to be considered.
1. The temperature is below the critical temperature. At or below this
temperature the resistance of the filaments vanishes (R
fil = 0
[Omega]). Equation (28.35) shows that in this case no current will flow
through the copper matrix.
2. If the temperature of the wire is above the critical temperature, the
current flow will change drastically. In this case, the fraction of the
current flowing through the copper is equal to
(28.36)
The copper matrix will carry 90% of the total current.
Example: Problem 28.42
What is the resistance of the combination of four resistors shown in
Figure 28.7. Each of the resistors has a value of R.
Figure 28.7. Problem 28.42.
To find the net resistance of the circuit shown in Figure 28.7, we start
calculating the net resistance R
34 of the parallel circuit of
resistors R
3 and R
4:
(28.37)
or
(28.38)
The circuit shown in Figure 28.7 is therefore equivalent with the circuit shown
in Figure 28.8. Resistors R
2 and R
34 form a series
network and can be replaced by a single resistor with a resistance
R
234 where
(28.39)
Figure 28.8. Problem 28.42.
Figure 28.9. Problem 28.42.
The circuit shown in Figure 28.8 can now be replaced by an
equivalent circuit shown in Figure 28.9. The resistance R
tot of
this circuit can be obtained from the following relation
(28.40)
or
(28.41)
In the special case considered, R
1 = R
2 = R
3 =
R
4 = R. Thus
(28.42)
(28.43)
(28.44)
For R = 3 [Omega] the total resistance is equal to 1.8 [Omega].
No comments:
Post a Comment